Why does my vessel need an inclining test, and how is it done?

The purpose of the inclining test, or inclining experiment as it is sometimes termed in naval architecture, is to determine the coordinates of the lightship centre of gravity of the vessel, and most importantly the position of the vertical centre of gravity (VCG) often referred to as KG in naval architecture terminology.
Knowing the position of the lightship centre of gravity is necessary in order to calculate the stability characteristics of the ship for variable loading conditions, and to determine whether the vessel meets the statutory stability criteria with which the ship needs to comply. These stability characteristics are then set out in a stability information book, which then needs to be submitted to the certifying authority for approval.

So how does inclining the ship allow us to determine the vertical centre of gravity KG?

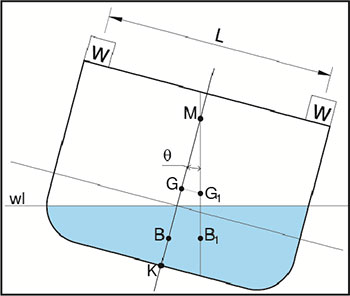
Well first of all the inclining results will yield the transverse metacentric height of the ship (GM). Referring to the diagram below, the metacentric height is equal to the distance between the metacentre M and the centre of gravity G.
The metacentre (M) is a function of the displacement of the ship, and represents the point of intersection of the line of buoyancy force as the ship is inclined through small angles of heel.

If M is above G the metacentric height is considered as positive, if below G, it is considered negative. The distance GM is taken as the measure of initial stability at small angles of heel, and for all ships in any condition of loading, GM should always be positive.

The inclining experiment is conducted as follows. A weight (W) is moved transversely across the deck through a known distance (L). This causes the ship to be inclined, and the angle of inclination can be measured by pendulums (or by other methods if agreed with the certifying authority).

As W is moved across the deck the centre of gravity of the ship moves from G to G1, such that:
WL = D GG1 where W = the mass of the inclining weight and D = displacement of ship in the inclined condition.

The ship will be inclined through some angle θ and will be in stable equilibrium in this position. The centre of buoyancy B was originally under G, but it will move to B1 to be in the same vertical line as G1. GG1 is parallel to the movement of W and thus the angle MGG1 is 90 degrees, and from trigonometry GG1 = GM tan θ. Therefore WL= D GM tan θ Or GM = (WL)/(D tan θ)

In the inclining experiment the values of W, L, D and tan θ are all known quantities, and thus GM may be calculated.

However, it is the value of KG that is to be determined, and referring again to the diagram, it can be seen that KM = KG+GM.
The value of KM is obtained from the hydrostatic data for the vessel at the as inclined displacement.

Using the value of KM from the hydrostatic data and the average value of GM, (usually 8 weight shifts are required to obtain a reliable data set) the value of KG can then be calculated as follows: KG= KM-GM